Unicode Normalization

Today I ran into an amusingly named place, thanks to some sharp eyes on the OpenStreetMap US Slack. The name of this restaurant is listed as ”𝐊𝐄𝐁𝐀𝐁 𝐊𝐈𝐍𝐆 𝐘𝐀𝐍𝐆𝐎𝐍“. That isn’t some font trickery; it’s a bunch of Unicode math symbols cleverly used to emphasize the name. (Amusingly, this does not actually show up properly on most maps, but that’s another story for another post).

I was immediately curious how well the geocoder I spent the last few months building handles this.

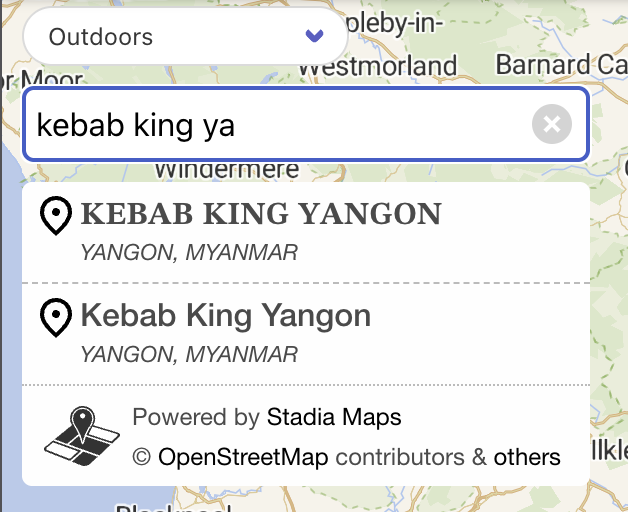
Well, at least it found the place, despite the very SEO-unfriendly name! But what’s up with the second search result?

Well, that’s a consequence of us pulling in data from multiple sources. In this case, the second result comes from the Foursquare OS Places dataset. It seems that either the Placemaker validators decided to clean this up, or the Foursquare user who added the place didn’t have that key on their phone keyboard.

One of the things our geocoder needs to do when combining results is deduplicating results. (Beyond that, it needs to decide which results to keep, but that’s a much longer post!) We use a bunch of factors to make that decision, but one of them is roughly “does this place have the same name,” where same is a bit fuzzy.

One of the ways we can do this is normalizing away things like punctuation and diacritics. These are quite frequently inconsistent across datasets, so two nearby results with similar enough names are probably the same place. Fortunately, Unicode provides a few standardized transformations into canonical forms that make this easier.

Composed and decomposed characters

What we think of as a “character” does not necessarily have a single representation in Unicode. For example, there are multiple ways of encoding “서울” which will look the same when rendered, but have a different binary representation. The Korean writing system is perhaps a less familiar case for many, but characters with diacritical marks such as accents are usually the same. They can be either “composed” or “decomposed” into the component parts at the binary level.

This composition and decomposition transform is useful for (at least) two reasons:

1. It gives us a consistent form that allows for easy string comparison when multiple valid encodings exist.
2. It lets us strip away parts that we don’t want to consider in a comparison, like diacritics.

I use the unicode_normalization crate to do this “decompose and filter” operation. Specifically, the UnicodeNormalization trait, which has helpers which will work on most string-like types.

Normalization forms

You might notice there are four confusingly named methods in the trait: nfd, nfkd, nfc, and nfkc. The nf stands for “normalization form”. These functions normalize your strings. c and d stand for composition and decomposition. The composed form is, roughly, the more compact form, whereas the decomposed form is the version where you separate the base from the modifiers, the jamo from the syllables, etc.

We were already decomposing strings so that we could remove the diacritics, using form NFD. This works great for diacritics and even Hangul, but 𝐊𝐄𝐁𝐀𝐁 𝐊𝐈𝐍𝐆 𝐘𝐀𝐍𝐆𝐎𝐍 shows that we were missing something.

That something is the k, which stands for “compatibility.” You can refer to Unicode Standard Annex #15 for a full definition, but the intuition is that compatibility equivalence of two characters is a bit more permissive than the stricter canonical equivalence. By reducing two characters (or strings) to their canonical form, you will be able to tell if they represent the same “thing” with the same visual appearance, behavior, semantic meaning, etc. Compatibility equivalence is a weaker form.

Compatibility equivalence is extremely useful in our quest for determining whether two nearby place names are a fuzzy match. It reduces things like ligatures, superscripts, and width variations into a standard form. In the case of ”𝐊𝐄𝐁𝐀𝐁 𝐊𝐈𝐍𝐆 𝐘𝐀𝐍𝐆𝐎𝐍,” compatibility decomposition transforms it into the ASCII “KEBAB KING YANGON.” And now we can correctly coalesce the available information into a single search result.

Hopefully this shines a light on one small corner of the complexities of unicode!